These were the topics discussed.
Spatial Relationships are having a picture of a number including where it lies on a number line.
One/Two More/Less: If you have 5/4, what is 1/4 more/less? What is 2/4 more/less?
ex: 5/4 + 1/4 = 6/4, 5/4 - 1/4 = 4/4 = 1, 5/4 + 2/4 = 7/4, 5/4 - 2/4 = 3/4
Benchmarks of 0, 1/2, and 1... is it about or below 1/2? How far away is it from 1?
Part-Part-Whole: Knowing 3/4 can be (1/2+1/4) or (1/4+1/4+1/4)
ex: 7/5
Spatial Relationship:
One/Two More/Less:
7/5 + 1/5 = 8/5, 7/5 - 1/5 = 6/5, 7/5 + 2/5 = 9/5, 7/5 - 2/5 = 5/5 = 1
Benchmarks: More than 1, 1 + 2/5 = 7/5
Part-Part-Whole:
(1/5+1/5+1/5+1/5+1/5+1/5+1/5), (1+2/5), (2-3/5)
One Thursday we went over showing how to represent fractions in diagrams
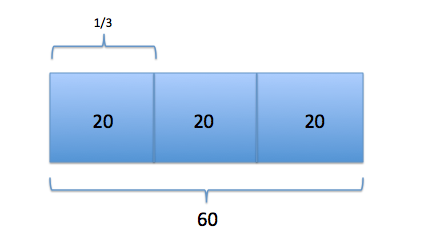
Running Task: If I ran 1/3 of an hour and then walked for 1/4 of an hour, how much time would that be? What fraction of an hour is that?
They ran for 20 minutes + 15 minutes, thats 35 minutes total or 35/60 minutes.
The Clock Model
Traditional Method of Adding and Subtracting Fractions:
ex: 15 3/8 + 11 7/16
15 3/8 15 6/16
+ 11 7/16 ----> + 11 7/16 ----> 26 13/16
15 3/8 15 6/16
- 11 7/16 ----> - 11 7/16 ----> 3 15/16



I liked how much you touched on benchmark numbers to easily identify how big or small a fraction is. In class it seemed like people struggled to quickly figure out which fraction was bigger, but you did a great job of breaking down how to compare it to whole numbers and their halves. You had a really good use of images that added to your blog.
ReplyDelete- Sam Gaume
I loved your pictures for the clock and hour models we learned. I would have liked to see pictures for the other explanations, but overall this was a good blog. Spacial relationships with fractions can be hard to see and with the use of your picture and explanation I think you were effectively able to explain it. Good job!
ReplyDelete